Suite de Fibonacci - Graphique pour dessiner des spirales

Leonardo Pisano Fibonacci est un mathématicien italien qui a vécu en plein âge d'or des Cathédrales (XIIe et XIIIe siècles).

A cette époque des échanges importants on lieu entre l'Europe et le monde musulman.

les chiffres arabes font leur entrée discrète parmi les plus érudits, le voyageur et mathématicien Fibonacci a contribué à leur adoption et leur développement.

L'abaque utilisé par ses contemporains n'utilise pas le 0, les chiffres arabes permettent une révolution numérique qui servira à la réalisation des ouvrages d'art les plus complexes.

Fibonacci est surtout connu pour sa suite : 1,1,2,3,5,8,13,21,34...

Ces nombres correspondent à une démonstration faite sur l'étude de la progression des générations de lapins sur une échelle mensuelle.



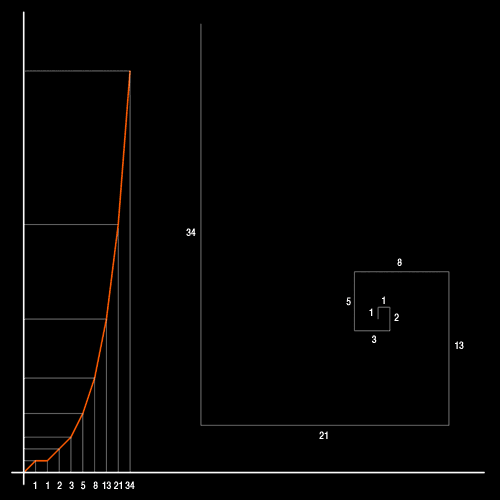
Cette courbe logarithmique se vérifie à chaque fois que des lapins sont lachés sur une île favorable à leur développement.

Le graphique marque au passage la puissance de la croissance naturelle qui en l'absence de contraintes atteint rapidement des proportions extraordinaires.

Dans l'exemple des lapins, la mortalité n'est pas prise en compte.

D'autres organismes vivants comme les bactéries et virus ont cette capacité de division ou réplication rapide qui va se caractériser par une courbe logarithmique.

Au niveau mathématique, on notera que chaque terme de cette suite est la somme des deux précédents selon un principe de récurrence.

Sur le graphique on voit que la progression de la suite de Fibonacci forme des lignes brisées au début.

Si on trace une spirale à partir des points elle ne sera pas des plus esthétiques au niveau du centre, mais ensuite on se rapprochera de la belle forme que l'on retrouve dans la coquille du nautile.



Dans la suite de Fibonacci le rapport change à chaque quart de tour, mais va tendre vers le nombre d'or (1,618...). Si on veut donc réaliser une spirale parfaite sur ce type de rapport, il est préférable d'utiliser le nombre d'or.

Cela demande d'utiliser des outils, une calculette pour nous, un compas d'or pour les constructeurs de cathédrales, une corde à noeuds pour les premiers architectes.

Les frondes de fougères sont proches de ce graphisme car le pétiole enroulé est plus large à la base que vers la pointe.

Le rayon de rotation varie donc plus doucement que celui de la coquille d'un nautile.



Voici comment construire une spirale simple sans le nombre d'or :

• Tracer un carré
• Mettre la pointe du compas sur un des angles, le crayon sur l'angle suivant
• Tracer un quart de cercle en partant du carré vers l'extérieur
• Déplacer la pointe du compas sur l'angle le plus proche (dans le même sens que la rotation de votre spirale).
• Placer le crayon sur l'extrémitée de la spirale et tracer un quart de cercle
Etc...

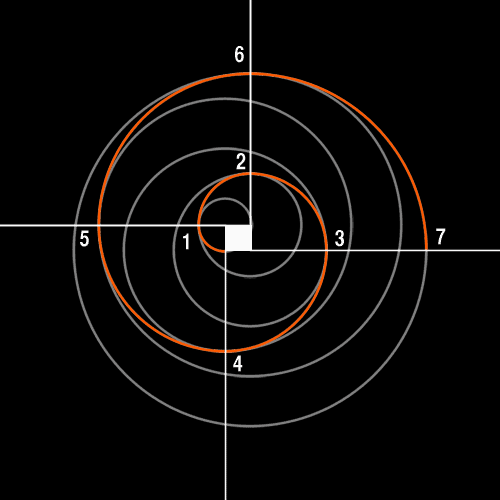
Cette spirale n'utilise pas la suite de Fibonacci mais c'est la plus facile à dessiner.

La spirale du site de la Nazca au Pérou est un géoglyphe de 80 m environ, il témoigne de connaissances géométriques antérieures à -300 av JC.

Les deux spires dessinées sur le sol n'utilisent pas le nombre d'or, l'écartement entre chaque sillon reste régulier, le tracé utilise un module que l'on retrouve au centre.

Selon le type d'outil utilisé, Le dessin peut comporter des raccords ou se dérouler de manière harmonieuse

Pour faire une spirale parfaite, il faut pouvoir recalculer la position de chaque point par rapport au centre, ce qui se fait avec un ordinateur lors de l'utilisation d'outils vectoriels.

Avec des moyens plus simples : une corde enroulée autour d'un baton permet de faire une belle spirale parfaite.



Dans l'architecture :

Le minaret de la grande mosquée de Samarra construit au 9ème siècle a un plan en spirale qui se développe en hauteur.

On retrouve cette forme amplifiée dans la peinture "La Tour de Babel" de Pieter Brueghel l'Ancien (16ème siècle). Le motif architectural serré au centre se développe dans les deux dimensions en formant un tourbillon proche des forces naturelles (eau, vent...).



Dans la nature, les feuilles, pétales ou bractées se développent en rotation autour d'un axe en suivant des angles remarquables et notamment celui formé par le nombre d'or.

Quand ces éléments se massent à l'extrémité d'une plante, l'organisation doit être parfaite et s'organise généralement en spirales concentriques.

Triskel (3 spires) et svastika (4 potences) sont des symboles utilisant comme trame plusieurs spirales concentriques :

Il peuvent être dextrogyres (rotation à droite) ou lévrogyres (rotation à gauche). Dans les deux cas les origines de ces symboles sont très anciennes.

Les lobes de pervenche sont dextrogyres.

Un même centre peut être à l'origine de spirales dextrogyres et lévrogyres, c'est souvent le cas pour les plantes :

• Capitules d'astéracées
• Certaines crassulacées

Le symbole international "Danger biologique" comporte des boucles dextrogyres et lévrogyres inscrites dans un triangle.

On retrouve à ce stade une inquiétude de l'homme pour une propagation biologique exponentielle, ce qui nous ramène directement au lapin de Fibonacci.



Autre sources d'informations sur Fibonacci, les spirales ou le nombre d'or :

• Corde à treize noeuds (Wikipedia.org)
• Suite de Fibonacci (Wikipedia.org)
• Les angles privilégiés (Persee.fr)
• Les tracés de Nazca (Dinosoria.com)
Le Nautile dans l'Art

Voici une superbe vidéo de ETEREA Studios par Cristóbal VILA qui illustre mieux qu'un long discours la magie de la suite de Fibonacci: